regrake: Regularized Raking in R

My new R package regrake is now live!

Regularized raking enables more flexible functional forms in raking to population targets, supports meaningful regularization, and ultimately leads to more expressive and efficient survey weights.

You can install the package from GitHub (CRAN coming soon):

remotes::install_github("andytimm/regrake")

The rest of this post gives a light overview of the problem regularized raking solves, and introduces some interface elements I’m excited by.

Flexible raking and regularization

Survey researchers increasingly ask a lot of our weights. We know our sample can be subtly or not so subtly unrepresentative in hard to fix ways, and expansive weighting schemes, no matter how imperfect, are part of the toolkit to address these challenges. Take, for example, the growing list of weighting variables in any recent NYT survey¹.

What does this have to do with how exactly we fit our weights, though?

I find an analogy to predictive modeling instructive here. The early calibration literature like Deville & Särndal (1992) makes it pretty clear that raking can be roughly understood as linear regression on the weighting problem². Like with linear regression in the predictive context, we can add more marginal terms and interactions to (perhaps) fit a better model. Layering in more and more predictors like this allow one to extract further signal from your data, but you’ll quickly begin to feel the inflexibility of the regression framework as problems get more complex.

Pushing all the way to a highly flexible, probably Bayesian or machine learning model to pull more signal out of available data without a variance explosion works, but often a simple lasso, ridge, or horseshoe prior regression model provides most of the additional signal for minimal additional effort. I think the regularized raking available in regrake offers a compelling level of flexibility without much more implementation complexity.

Here’s an example: In the 2016 pew study I’m weighting in the slides below, we should have some intuition that getting Trump vote choice right is relevantly about not just marginal distributions of weighting dimensions like age, gender, race, region, and education, but also many interactions between these — whomst amongst us hasn’t worried about non-college midwestern whites? However, a more fully interacted model won’t³ converge with basic raking, and the nearby partial solutions pay a relatively large variance cost⁴.

A sensible path forward available with regularized raking is to still require exact matching on all the marginal distributions, but optimize for merely least squares close target adherence on relevant 2 and 3-way interactions. When combined with some relatively light touch regularization, we end up with pretty clean target adherence:

being 1pp off targets on the harder margins isn’t bad at all!

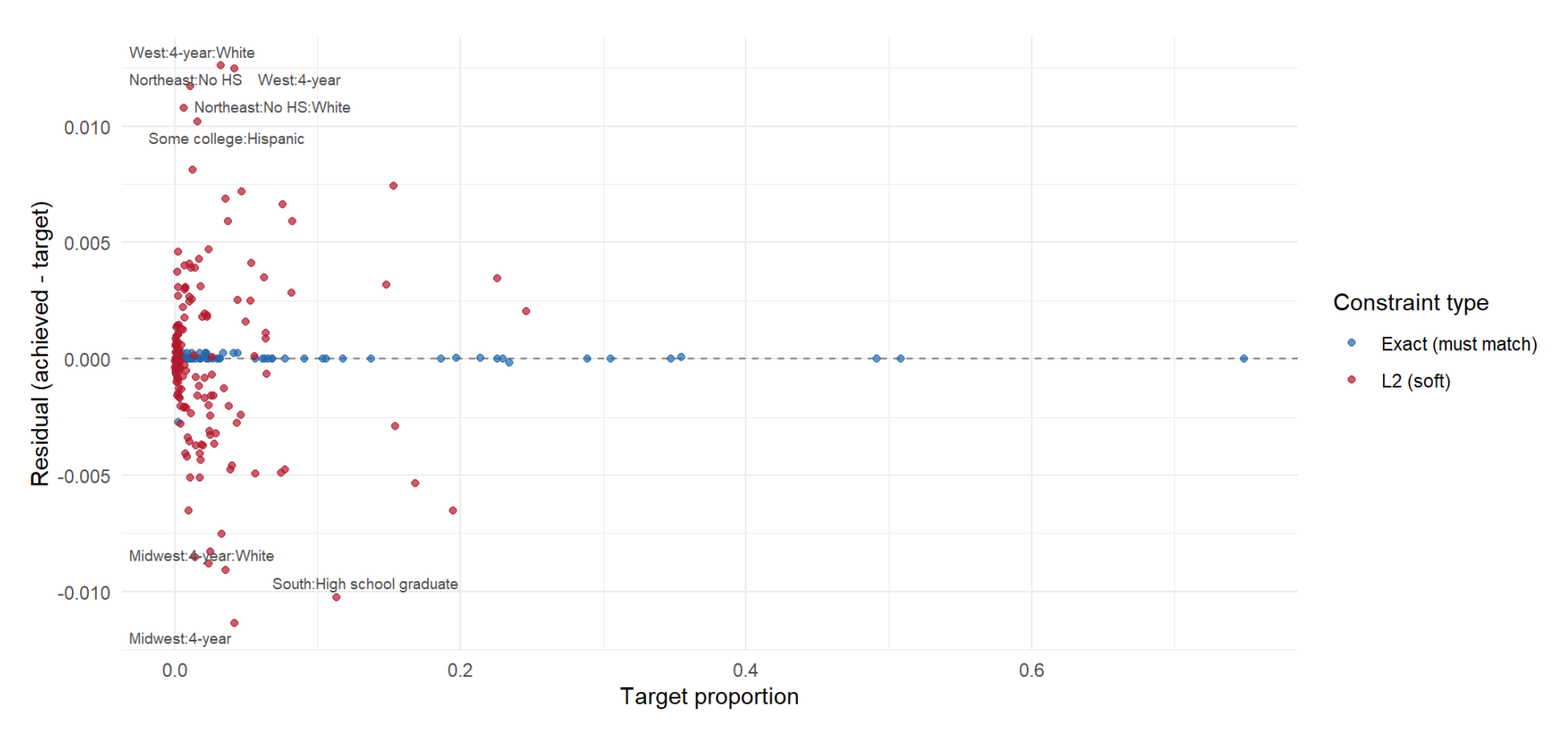
While there are certainly applications that call for going all the way to something more complex like MRP, my sense is regularized raking can deliver much of the incremental benefit at lower effort. Coming back to that predictive modeling analogy, the sample you start with and the variables you choose to weight on still matter more than anything about how you weight, but more expressive tools give you better action space.

Formula interface

I’ve always been inspired by the elegance of brms’s formula interface: Even complex models feel pretty easy to express elegantly. I’ve tried to capture some of that experience here.

regrake makes it pretty easy to specify relatively complex constraints, like a mix of exact constraints on marginal totals and L2 constraints on interactions:

regrake(
  data = survey_data,
  formula = ~ rr_exact(recode_age_bucket) + rr_exact(recode_female) +
              rr_exact(recode_inputstate) + rr_exact(recode_region) +
              rr_exact(recode_educ) + rr_exact(recode_race) +
              rr_l2(recode_region:recode_educ) +
              rr_l2(recode_region:recode_race) +
              rr_l2(recode_educ:recode_race) +
              rr_l2(recode_region:recode_educ:recode_race),
  population_data = pop_targets,
  pop_type = "proportions",
  regularizer = "entropy",
  lambda = 10
)

Swapping a constraint from rr_exact() to rr_l2(), or tweaking lambda to adjust regularization, is a one-line change, which makes it easy to iterate and compare.

Target Input Interfaces That Don’t Suck

Structuring weighting target inputs in R has always been moderately annoying to me. One thing I’m happy with here is that I’ve been able to support a pretty wide set of input formats.

For example, I find the autumn df format pretty elegant:

targets <- tibble(
  variable = c("sex", "sex", "age", "age",
               "sex:age", "sex:age", "sex:age", "sex:age"),
  level    = c("M", "F", "young", "old",
               "M:young", "M:old", "F:young", "F:old"),
  target   = c(0.49, 0.51, 0.45, 0.55,
               0.20, 0.29, 0.25, 0.26)
)
targets

# A tibble: 8 × 3
  variable level   target
  <chr>    <chr>    <dbl>
1 sex      M         0.49
2 sex      F         0.51
3 age      young     0.45
4 age      old       0.55
5 sex:age  M:young   0.20
6 sex:age  M:old     0.29
7 sex:age  F:young   0.25
8 sex:age  F:old     0.26

But the package is just as happy to take an anesrake style list:

targets <- list(
  sex       = c(M = 0.49, F = 0.51),
  age       = c(young = 0.45, old = 0.55),
  `sex:age` = c(`M:young` = 0.20, `M:old` = 0.29,
                `F:young` = 0.25, `F:old` = 0.26)
)
targets

$sex
   M    F
0.49 0.51

$age
young   old
 0.45  0.55

$`sex:age`
M:young   M:old F:young   F:old
   0.20    0.29    0.25    0.26

Or a poststratification table:

pop_table <- tribble(
  ~sex, ~age,     ~count,
  "M",  "young",  2000,
  "M",  "old",    2900,
  "F",  "young",  2500,
  "F",  "old",    2600
)
pop_table

# A tibble: 4 × 3
  sex   age   count
  <chr> <chr> <dbl>
1 M     young  2000
2 M     old    2900
3 F     young  2500
4 F     old    2600

These are ultimately all converted back to the autumn format for use. My hope is that this fluidity with inputs makes it a bit easier to try regularized raking on your data.

Learning More

If this has piqued your interest, a good longer introduction to regularized raking is these slides, a slightly updated version of a talk I gave at NYOSPM.

If the underlying optimization logic is interesting to you, I’d check out Barratt, Angeris, and Boyd (2021)- it’s a really clean, elegant application of alternating direction method of multipliers (ADMM) ideas and super readable.

Footnotes

1. Check out this long list of weighting variables- many of which my mentors from an earlier era of polling would find anathema to weight on! Source: NYT/Siena National Poll Toplines, January 2026

2. I’m being a little loose here in service of keeping the post going. If you take away “raking has linear regression vibes”, and “regularized regression has lasso/ridge/horseshoe vibes” I’m happy. More precisely, Deville & Särndal show that all calibration estimators, raking included, produce point estimates asymptotically equivalent to the generalized regression (GREG) estimator, which adjusts the Horvitz-Thompson estimator via a linear regression on the calibration margins. So raking on age and sex separately implicitly fits a main-effects-only linear model; no interactions. The weights themselves differ across calibration distance functions (raking guarantees positivity, for instance), but the estimates converge IIRC.

3. For anybody else who reads “won’t” as a challenge here, I’m aware of the various tricks one can resort to here. Picking and choosing interactions to keep, raking in stages, or being flexible with what “converged” needs to mean…. all these could probably get something close to the example to fit. The example is (deliberately) just simple enough that vanilla raking starts to struggle- you could force it to work. My claim here is that you shouldn’t have to resort to these sometimes hacky tricks we’ve collectively figured out: instead, try to formalize the solution you actually want, and optimize against that.

4. Similar to the above footnote, if your reaction here is that you’ve got plenty heuristic tools like trimming or winsorization to bring down that variance/deff cost, again my claim is that you shouldn’t have to do this. Instead, you can write down the optimization problem you actually want to solve, weighting induced variance limitations included, and directly solve that.